今日からは何回かに分けて、データの見せ方、つまりグラフについて書きたいと考えています。
初回はヒストグラム。非常に重要ながら意外と描かない(描けない)という話も耳にします。
こんなグラフ
ヒストグラムは、ある数値幅(ビンといいます)に入るデータがどれくらいあるか、というものを棒の高さで表すグラフです。このようなグラフを描くことで、値がどんな範囲にどのような形でばらついているかを一目で知ることができます。とにかく、まとまったデータが手に入ったときにはまず最初に見ておく、くらいのスタンスでもいいほど有用なグラフです。
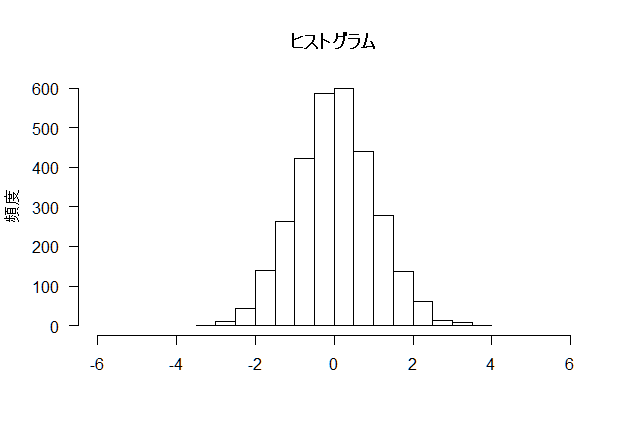
これは、3000個の数値をヒストグラムにしたものですが、
- このデータは大体-4~4の範囲に値が分布していて、
- その分布は0を中心として左右対称。
- ほとんどが0の周り、-2~2の範囲に集中している。
- ばらつき方に大きな偏りもなく、
- おそらく正規分布だろうな
といったことが一目で分かります。(実際この数値は標準正規分布乱数です)
Rで描いてみる
Rでは、hist(x)で簡単に書くことが出来ます。xにはデータベクトルが入ります。MASS::truehist(x)を使う人もいますね。ひとまず、ちょっと描いてみます。
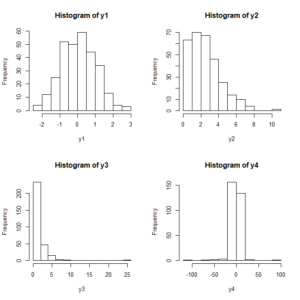
set.seed(3) y1 <- rnorm(300, 0, 1) #標準正規乱数を300個用意 y2 <- rpois(300, 3) #λ=3のポアソン分布に従う乱数300個用意 y3 <- rlnorm(300, 0, 1) #対数正規分布に従う乱数を300個用意 y4 <- rcauchy(300) #コーシー分布に従う乱数を300個用意 par(mfrow=c(2, 2)) #描画デバイスを4分割 hist(y1) #ヒストグラムを描く 以下同じ hist(y2) hist(y3) hist(y4)
こんな感じですね!それぞれの分布の雰囲気が表れています。ここ数年はなんだかちょっと統計が流行っていて、特に所得分布(※所得は対数正規分布に従います)などの話で「平均値より中央値」などといった話が出てきたりしますが、統計量のみを書いてあーだこーだ言うくらいなら初めから全体の分布を描いてしまえばいいと思います。というわけで、検討したい変数についてはまずヒストグラムを描いてしまいましょう。
ヒストグラムで比較
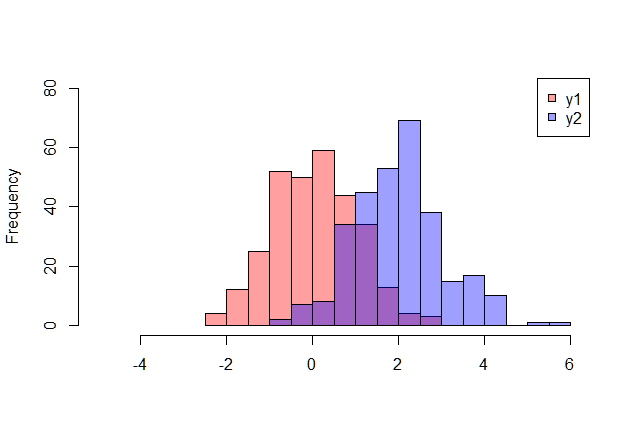
ヒストグラムはデータを比較することもできますが、多くの変数を一度に比較する用途にはあまり向きません。また、描画に多少の工夫が必要です。さらにはデータの分散が大きく違ったりするとビンの幅が変わって見にくくなることもあります。
set.seed(3)
y1 <- rnorm(300, 0, 1)
y2 <- rnorm(300, 2, 1)
hist(y1, xlim=c(-5, 6), col="#FF000060", main="", ylim=c(0, 80), xlab="")
hist(y2, col="#0000FF60",add=T)
legend("topright", pch=22, pt.bg=c("#FF000060", "#0000FF60"),
legend=c("y1", "y2"))
(余談)ExcelからコピーしてRでヒストグラム
ヒストグラムはExcelなどでは書きづらいという話もあります。よくわかります。「分析ツール」とか選んでデータ範囲を選択して幅を決めて……という煩雑な操作が必要なんですよね。今は改善されていたりするのでしょうか。素直にRを使った方が速いと思います。で、Excelからコピペみたいに描けないのかと過去に訊かれたことがあります。さっと見る程度ならこういう方法はあります。
1.Excel上でヒストグラムを描きたいデータ列があるとします
2.データ列、範囲を選択し、Ctrl+Cでコピーしてクリップボードに取り込みます

3.Rで以下のコードを実行
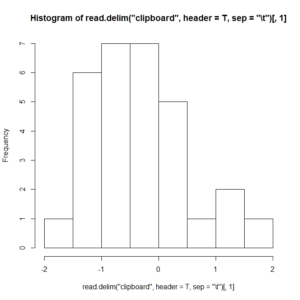
hist(read.delim("clipboard", header=T, sep="\t")[,1])
4.描けます。
選択したデータ領域にデータの変数名(header)がない場合は、header=Fとしましょう。こんなことするくらいならちゃんとRでデータを読み込んで操作した方が早い気もしますけど……。
ヒストグラムの利点と難点まとめ
◆ヒストグラムの利点
- データの分布が一目でわかる。つまり、
- データがどの範囲にわたって存在しているか(レンジ)
- よくある値(最頻値)がどこか
- どのようにばらついているか(分散)
- おおよそどんな分布に従っているか
- …といった様々な情報が視覚的に分かりやすい
◆ヒストグラムの難点
- 描くのにある程度まとまった量のデータが必要
- 描くのが面倒(?)
- あまり多くの変数を比較したりする用途には向かない
とにかくデータが手に入ったらまずヒストグラムを見て分布を確認してみましょう。なんというか、挨拶みたいなものです。