更新の初回は線形回帰についてです。
PRML(パターン認識と機械学習)の3章で
正則化の図(図3.4)がよく分からなかった思い出から、
このあたりについてなるべくわかりやすい説明を書こうと思います。
1次式による回帰
係数が1次までの多項式線形モデルで回帰をすることを考えます。つまりy=ax + b みたいな直線で回帰するという話ですね。今日は以下のように書くことにします。
\[
{\bf y} = w_0 + w_1{\bf x}
\]
xとyはベクトルで、それぞれ説明変数と応答変数。w0(切片)とw1(傾き)が係数ですね。
さて、データへのあてはめを考えましょう。変数はw0とw1ですね。これらをいろいろと変えて、上の関係が「一番よくデータに当てはまる」w0とw1を探します。どうすれば上のモデルの「データへの『当てはまり』」をよくできるでしょうか?
そのためには、データのxから上のモデルでyを推定し、推定されたyと実際のデータのy(y’とします)との差を最小化することが考えられます。その基準として、推定されたyとy’の差の二乗(二乗和誤差)を合計して、これを最小化するのでしたね。これが最小二乗法です。
つまり、この問題はw_0とw1がいろいろ変わったとして、その時の二乗和誤差を最小化する問題なんですね。この問題に関しては式を変形していくことで厳密に解くことができるのですが、
今日はちょっとイメージ付のため別の解き方をします。実際に、w0とw1にいろいろな値を入れてみて、二乗和誤差が小さくなるところを探ってみます。
Rでのデータ生成、確認
では、Rで実際にデータを生成してみます。
set.seed(10000) x <- runif(30, -5, 5) y <- 2 + x*1 +rnorm(30, 0, 1)
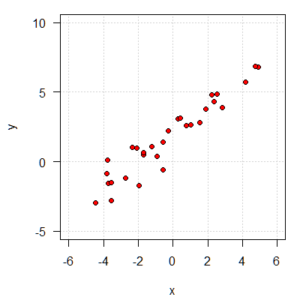
さあ、これでy = 2 + 1x +ε (εは標準正規分布に従うノイズ)という構造のデータを生成できました。グラフを見ておきましょう。
par(mar=c(4.2, 4.2, 1, 1))
plot(x, y, pch=21, bg=2,
xlim=c(-6, 6), ylim=c(-5, 10),
las=1, panel.first = grid())
dev.off()
いかにも、一次式でいい感じにモデル化できそうですね。
係数を変えて、当てはまり(の悪さ)計算
では、実際にw0とw1にいろいろな値を入れてみて、その時の二乗和誤差関数EDを計算、このときのw0, w1, をimageでグラフとして表してみます。
w0 <- w1 <- seq(-5, 5, 0.05)
ED <- matrix(0, length(w0), length(w1))
for(i in 1:length(w0)){
for(j in 1:length(w1)){
yh <- w0[i] + w1[j]*x
ED[i, j] <- sum((y-yh)^2)
}
}
par(mar=c(4.2, 4.2, 1, 1))
image(w0, w1, ED, col=rev(rainbow(10000)[1:6500]), las=1)
points(2, 1, pch=22, bg="red", cex=2)
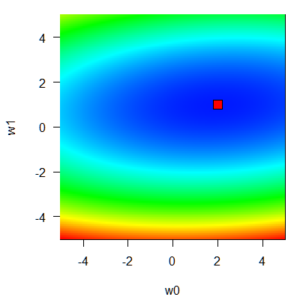
さて、図では残差二乗和が低くなるほど青色に、高くなるほど赤色になるように描画してあります。赤色の四角点は、データを生成させたモデルの係数、いわば「真のモデルの係数の点」のようなところですね。すなわちw0 = 2, w1 = 1です。実際におおよそここが極小点になっていることが分かりますね。
こういった曲面上での最小点を探せば、モデルの係数が決まるということになります。何気なく使うこともある一次式の線形回帰、そして最小二乗法の背景にはこういう話があるとイメージできると、話が理解やすくなると思います。(余談)w0方向は緩やかなのに、w1方向の傾斜は急ですね。これは今見ているw0とw1の範囲では、切片と比較して、傾きの変化が当てはまりに強く影響していることを示しています。
今日の重要な点は、係数をいろいろ変えたときに「当てはまりの悪さ」である残差二乗和が変わるんだ、という関数を具体的にイメージできるようになることです。次回は、ここを足掛かりに「正則化」のイメージについて書きます。