正則化?
では、今回は正則化の話に入っていきます。正則化は、PRMLでは例えば以下のような式で書かれています。
\[
\frac{1}{2}\sum_{n=1}^N \{t_n-{\bf w}^{\bf T}\phi({\bf x}_n)\}^2 + \frac{\lambda}{2} \sum_{j=1}^M |w_j|^q
\]
PRMLの(3.29)ですね。私は数学が苦手だったので、この式をはじめ見たときに「???」という感じだったのですが、落ち着いてみていけばそこまで複雑なものではありません。左の項は、前回やった二乗和誤差そのものです。1/2がかかっていますが、これは計算上の都合のものなので、あまり気にしなくていいです。前回やった係数が1次までの多項式の回帰の例では、左の項は以下のようになります。
\[
\frac{1}{2}\sum_{n=1}^N \{t_n-(w_0 + w_1 {\bf x}_n)\}^2
\]
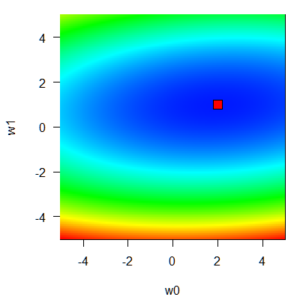
前回の記事で、最後に描いた二乗和誤差関数を思い出して下さい。w0とw1を変数として二乗和誤差は定まり、モデルの当てはまりがいい場所ではその値が小さくなる、という関数でしたね。
前回の例ではこの楕円すり鉢の底、極小点が求めたい場所なのでした。
さて、右の項です。これは、係数を除けば単純に係数の絶対値をq乗してその和をとっていることになります。今回の例でいえば、
\[
\frac{1}{2} \{|w_0|^q + |w_1|^q\}
\]
ということになります。これが一体どういう意味なのか。
正則化項の「形」
さて、w0とw1の絶対値のq乗和をq=2として、誤差関数と同じようにプロットしてみます。
w0 <- w1 <- seq(-5, 5, 0.05)
q <- 2
EW <- matrix(0, length(w0), length(w1))
for(i in 1:length(w0)){
for(j in 1:length(w1)){
EW[i, j] <- sum(abs(w0[i])^q + abs(w0[j])^q)
}
}
par(mar=c(4.2, 4.2, 1, 1))
image(w0, w1, EW, col=rev(rainbow(10000)[1:6500]), las=1)
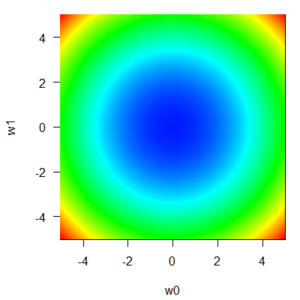
原点w0 = w1 =0 を中心とした、お椀型の関数になっていることが分かります。これが、q=2の正則化項のイメージです。青色であれば正則化項の値は低く、赤色であれば正則化項の値が高いのは前回の二乗和誤差関数の表示と同じですが、色と値の対応関係については前回の誤差関数とスケールが一緒ではありません。具体的に今回の例で言うと、二乗和誤差は10~4000くらいのレンジで変化しているのに対し、λ=1の正則化項のレンジは0~25くらいです。このスケールの違いを調整するためにλがあるとも言えます。とにかく、誤差関数の話と同じく、w0とw1の値によっていろいろ値が変わる関数なんだ、というイメージを持っておくことが重要です。
正則化項は何をするのか
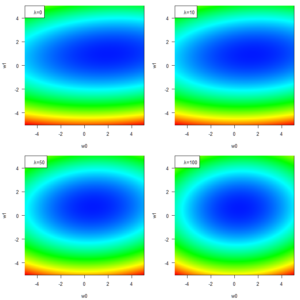
正則化項は、二乗和誤差との和として誤差関数となることにより「誤差関数全体を、原点を中心として底上げ」する作用があります。その底上げの程度はλの値によって変わります。実際の様子を見てみましょう。
順番に、λ = 0, 10, 50, 100です。λが大きくなるほど、正則化項の作用が強くなっています。
正則化項の作用が強くなってくると何が変わっているのでしょう?そう、誤差関数全体の形が正則化項の形に近づくように調整され、最小点も変わっているんですね。この場合、正則化項は原点を中心とした蟻地獄のような形をした関数ですから、大まかには各係数wの値を原点に寄せる効果があります。つまり、各係数が極端に大きな値にならないように調整するという役割があるということです。
この例だと、いったい何の役に立つの?という感じですよね。今は1次式モデルで十分に傾向を説明できていますし、おそらく今後データが増えてもそれほど予測精度が悪いという事態は生じないでしょう。正則化項が顕著にモデルの予測性能を改善してくれるのはより複雑なモデルを採用している場合が主です。例えば、より次数を上げた多項式などですね。複雑なモデルでも、正則化項の導入によってモデルが極端に学習データに合わせこみすぎないようにすることができます。これによっていわばより一般的なデータの傾向をとらえたモデルをつくることができ、汎化性能(未知のデータに対する予測性能)を上げることができる、というのが正則化項の狙いです。
次回はいろいろな正則化の形を見ていきます。