正則化項の形
さて、qをいろいろと変えてみたときの、正則化項のふるまいについてみておきます。
\[
\frac{\lambda}{2} \sum_{j=1}^M |w_j|^q
\]
実は、特定のqをもつ正則化項については特別な名前がついています。
いずれも今回の例としてwが二つ(w0, w1)のときまでを描画していますが、wがいくつになっても同様に定義されます。ただ3つ以上になるとわかりやすくは図にできないので……。
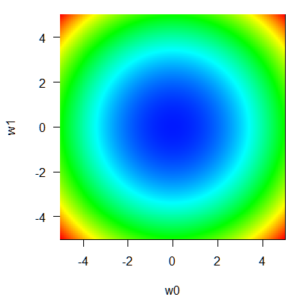
q=2:Lasso(ラスー)
前回も見たものですね。すり鉢というか、お椀型をしています。lassoというのは「投げ縄」のことで、輪っかの範囲に係数を束縛するみたいな意味合いでつけられた名前なのでしょう。
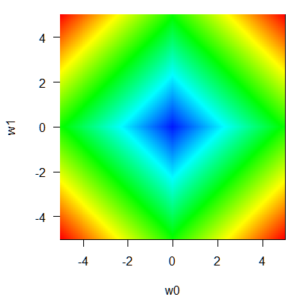
q=1:Ridge(リッジ)
リッジはw=0のところに尾根を持つ逆ピラミッドの形をしています。この尾根(というか谷というか)によって、係数を0付近に強く近づける作用があり、変数選択(効いていない、効きが弱い係数を0にしてしまう)の効果が得られます。ridgeというのは、まさに山の尾根のことです。
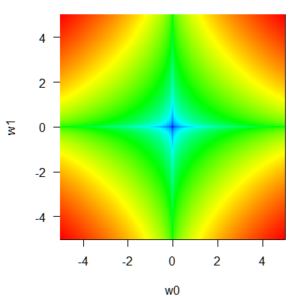
q=0.5:Elastic net(エラスティックネット)
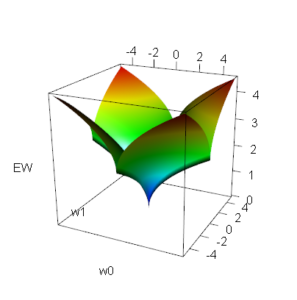
エラスティックネットはリッジよりさらに強く係数を0付近に近づける作用があります。persp3dなどを使って3次元の図を書くと、結構きれいな形をしており面白いです。
↑こんな感じですね。
とにかく、この例ではwoとw1に対して正則化項の値が決まる、という3次元的なイメージが持てることが大事です。これと二乗和誤差との和を誤差関数として最小化する問題にすることで、係数をあまり大きくしないようにする、あるいは0にしてしまう…という制約を与えることができるというのが、正則化の理解の第一歩です。
Rのコード
自分もRで上の図を再現してみたい!という方は以下を実行してみてください。
par(mfrow=c(2, 2), mar=c(4.2, 4.2, 1, 1))
w0 <- w1 <- seq(-5, 5, 0.05)
q1 <- c(2, 1, 1/2)
par(mfrow=c(2,2))
par(mar=c(4.2, 4.2, 1, 1))
for(h in 1:length(q1)){
EW <- matrix(0, length(w0), length(w1))
for(i in 1:length(w0)){
for(j in 1:length(w1)){
EW[i, j] <- sum(abs(w0[i])^q1[h] + abs(w0[j])^q1[h])
}
}
image(w0, w1, EW, col=rev(rainbow(10000)[1:6500]), las=1)
}
なお、上のコード実行後に
rgl::persp3d(w0, w1, EW, col=rainbow(600)[floor((max(EW)-EW)*100)], las=1)
を実行すると、Elasticnetの立体図を見られます。マウスでくるくる動かせるので楽しいです。Rにrglが入っていない場合、install.packages(“rgl”)でパッケージを入れてください。