今日は箱ひげ図を紹介します。箱ひげ図は、ヒストグラムと同じくそのデータの「分布」、データのばらつき方を描いてくれるものです。
こんなグラフ
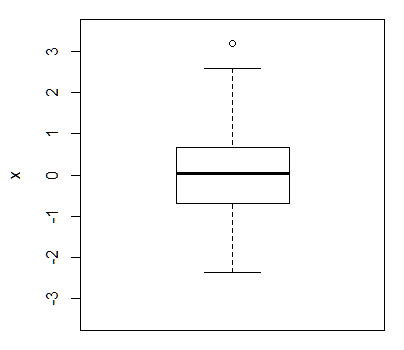
箱ひげ図は、Rではboxplot(x)で描けます。xはデータのベクトルです。見た目としてはこんなグラフとなります。
このグラフ、とにかくまずは見方を覚えてください。「箱」とその上下についた「ひげ」、それから「〇」全体でxという値の分布を表しています。ちなみにここでのxは300個の値を含んでいます。
- 太線で中央値(50%分位点)を表示
- 箱の上下端は、そのデータを小さい順に並べたときの75%分位点(上側)と、25%分位点(下側)を表す。
- すなわち、箱は中央値周り50%のデータの分布範囲を表す。
- この箱の上下方向の長さは四分位範囲(IQR)と呼ばれる統計量であり、データのばらつきを表す。
- 箱の上下端から外側1.5IQRの範囲までにすべてのデータが存在する場合、「ひげ」の端点は最大/最小範囲を表す
- 箱の上下端から外側1.5IQRを超える点にデータが存在する場合、ひげは箱の上下から外側1.5IQR点を表しすその範囲を超えるデータについては、丸(〇)で特別にプロットする。これは、簡単には「外れ値」気味の値を示しているととらえてよい。
- (つまり、上の図では下側の「ひげ」の端は最小値を表しており、上側の「ひげ」の端は75%分位点から1.5IQR外側点を示している)
たいへんややこしいので、ポイントを絞ります。
- 太線がデータの真ん中、中央値
- 箱の大きさはばらつき
- 箱の範囲に中央値周り50%のデータ、箱の上側に残りの25%、箱の下側に残りの25%のデータがある
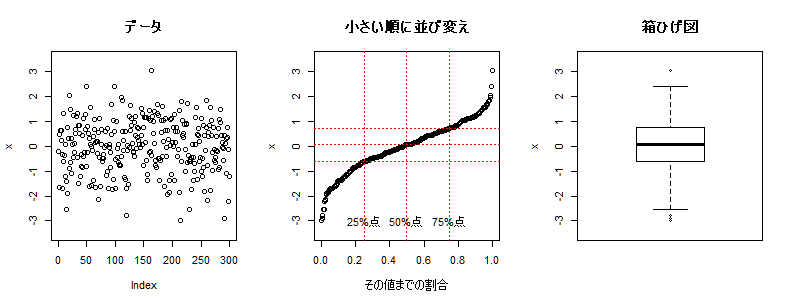
これでひとまずは十分です。イメージとして対応図を載せておきます。
比較に使いやすい箱ひげ図
箱ひげ図は分布を比較する用途、つまり因子を変えて値を測定、というような実験結果の図示に向いています。分散分析の対象になるようなデータですね。箱ひげ図を使うと効果が分かりやすくなります。大きな交互作用があるかどうかも簡単にチェックできます。
##仮データ作成
x1 <- 10 + 5 + rnorm(10, 0, 2)
x2 <- 20 + 5 + rnorm(10, 0, 2)
x3 <- 10 + 10 + rnorm(10, 0, 2)
x4 <- 20 + 10 + rnorm(10, 0, 2)
##データフレームづくり、因子の水準並び替え
data1 <- data.frame(nobi = c(x1, x2, x3, x4), water = rep(c("水やりなし", "水やりあり", "水やりなし", "水やりあり"), each=10), ferti = rep(c("肥料なし", "肥料あり"), each=20))
data1$water <- factor(data1$water, levels=c("水やりなし", "水やりあり"))
data1$ferti <- factor(data1$ferti, levels=c("肥料なし", "肥料あり"))
par(mar=c(9, 4.2, 1, 1)) #ラベルがはみ出すので調整
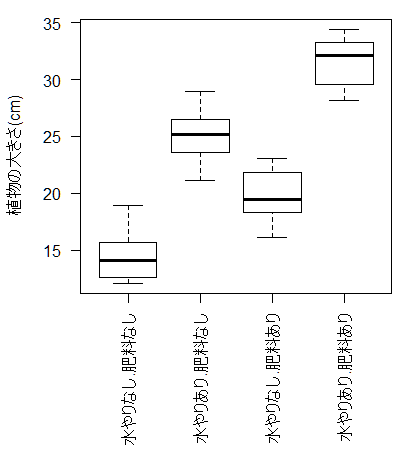
boxplot(nobi~water+ferti, data=data1, las=2, ylab="植物の大きさ(cm)") #ここでプロット
ぱっと見で水やり、施肥のあるなしの効果がどれくらいかわかりますし、大きな交互作用もなさそうだということが分かります。
空間データ(温度分布のような、スカラー量の空間分布データ)のようなデータも、ひとまず箱ひげ図で描いてみるとその空間上の関係性が見えて来やすいです。条件の違いによる値のふるまいを比較したいときに使いやすいということが箱ひげ図の特徴といえます。
箱ひげ図で気を付けたいこと
ヒストグラムと違って、分布の「形」は詳細にはわかりません。勝手に中央値に山があるような分布を想像してはいけません。
それから、箱ひげ図の意外な弱点は、他のグラフと比べると知っている人が少なくなってしまうことです。箱ひげ図でデータを見せたいときにはある程度説明を加えておく方が無難でしょう。あまりひげの定義とかに言及するとかえって混乱を招きますから、上の方に書いた3点くらいの説明をすれば十分でしょう。
また、箱ひげ図はExcelなんかでは描くのに多少の手間を要します。このブログではおそらく取り上げませんが、書き方を紹介しているウェブサイトもあるので調べてみてください。ただ、もうとにかくRを使うのがいいと思います(Rすき派)。
箱ひげ図の利点と難点まとめ
◆箱ひげ図の利点
- 値の分布の様子が大まかに分かる
- 値のレンジ、中央値などの分位点、と色々な情報が見える
- 複数の値の分布の比較がしやすい
- 実験条件の違いによる値の分布比較のような用途に向く
◆箱ひげ図の難点
- 分布の詳細な形までは分からない
- 見るのに多少慣れが必要
- 人に見せるときにグラフの説明が必要(かも)
本日の内容は以上です。